Σε ένα πλέγμα 2×2 τα πιθανά τετράγωνα που μπορούν να εμφανιστούν είναι πέντε. Αυτά φαίνονται στην παρακάτω εικόνα:
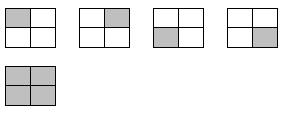
Ομοίως για ένα πλέγμα 3×3 το πλήθος των δυνατών τετραγώνων είναι 14:

Να γίνει αλγόριθμος, που θα διαβάζει το μέγεθος ενός πλέγματος NxN και θα υπολογίζει το πλήθος των δυνατών τετραγώνων που μπορούν να εμφανιστούν.
Ξεκινάμε με την εξής παραδοχή: Τα τετράγωνα που θα βρεθούν στο πλέγμα θα έχουν μέγεθος από 1 έως Ν. Έστω κ ή δεξιά πλευρά του τετραγώνου και λ η κάτω πλευρά αυτού. Αν μέγεθος_τ είναι το μέγεθος του εκάστοτε τετραγώνου, τότε οι πλευρές κ και λ θα ξεκινάνε από την μέγεθος_τ στήλη κσι γραμμή αντίστοιχα. Επίσης, καθώς μετακινούμε το τετράγωνο μέσα στο πλέγμα θα πρέπει να προσέξουμε ώστε να μην ξεφύγει από την Ν γραμμή και στήλη.
Ας δούμε τον αλγόριθμο:
Αλγόριθμος Πλέγμα
Διάβασε Ν
μέγεθος_τ <- 1
τετράγωνα <- 0
Όσο μέγεθος_τ <= Ν επανάλαβε
κ <- μέγεθος_τ
Όσο κ <= Ν επανάλαβε
λ <- μέγεθος_τ
Όσο λ <= Ν επανάλαβε
τετράγωνα ← τετράγωνα + 1
λ <- λ + 1
Τέλος_επανάληψης
κ <- κ + 1
Τέλος_επανάληψης
μέγεθος_τ <- μέγεθος_τ + 1
Τέλος_επανάληψης
Εμφάνισε "Πλήθος τετραγώνων: ", τετράγωνα
Τέλος Πλέγμα
